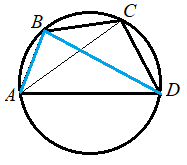
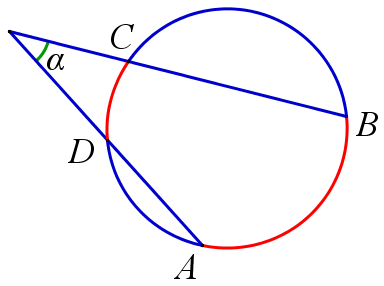
Как связан угол и дуга
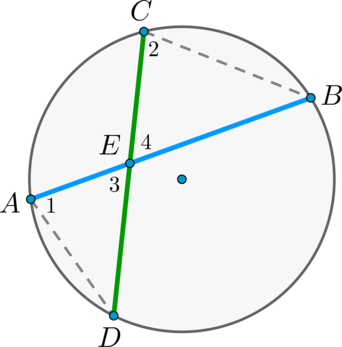
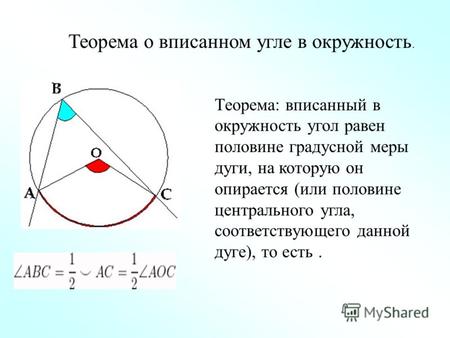
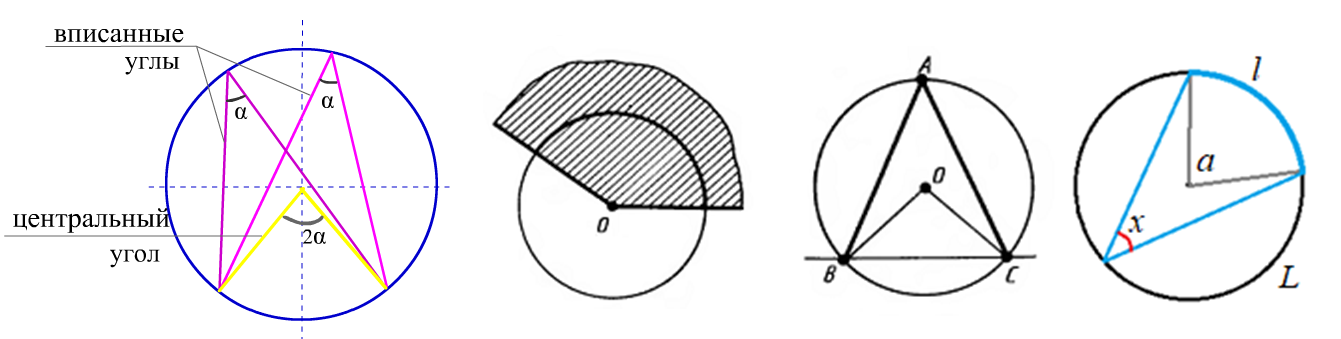
Вписанный и центральный угол окружности
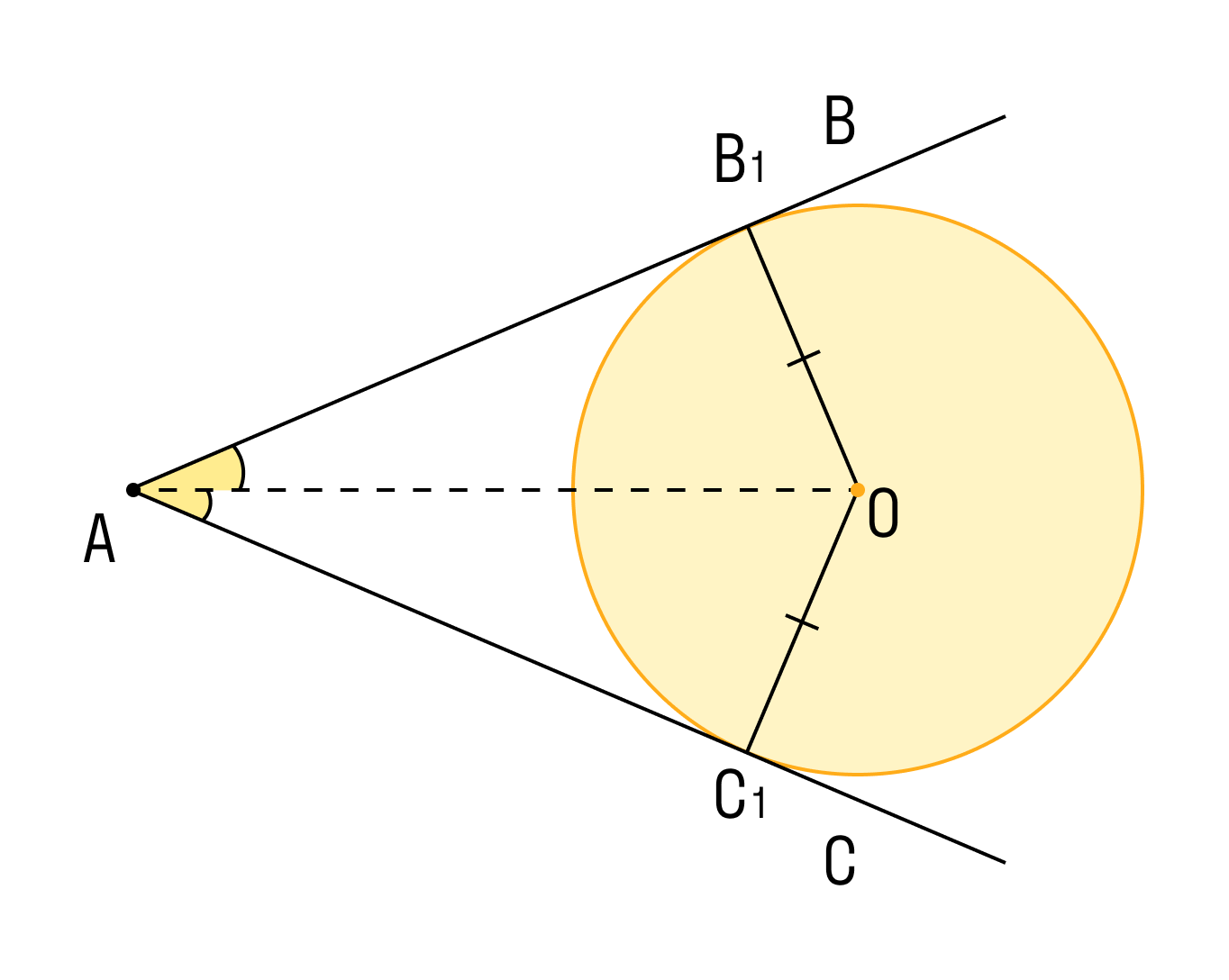
Доказательство проведём в два этапа: сначала докажем справедливость утверждения для случая, когда одна из сторон вписанного угла содержит диаметр. Возможны два случая:. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу. Такая прямая называется секущей.



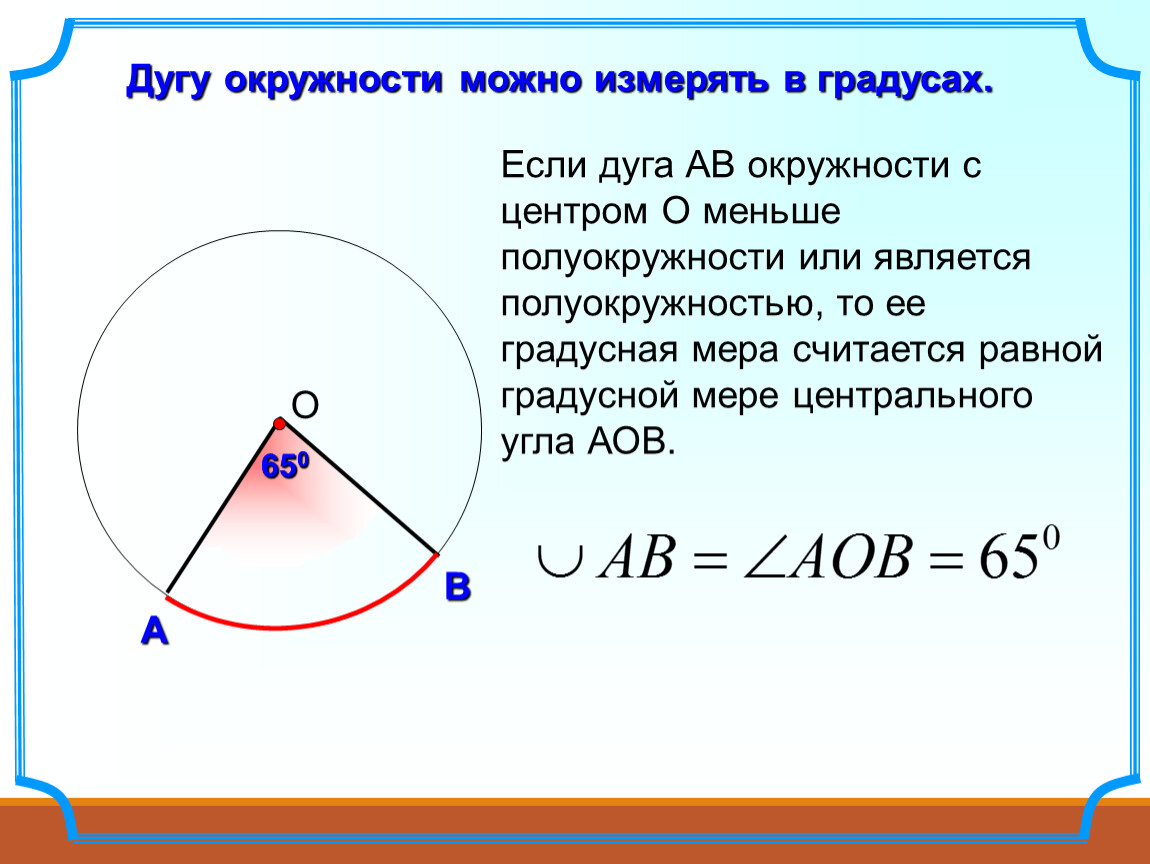

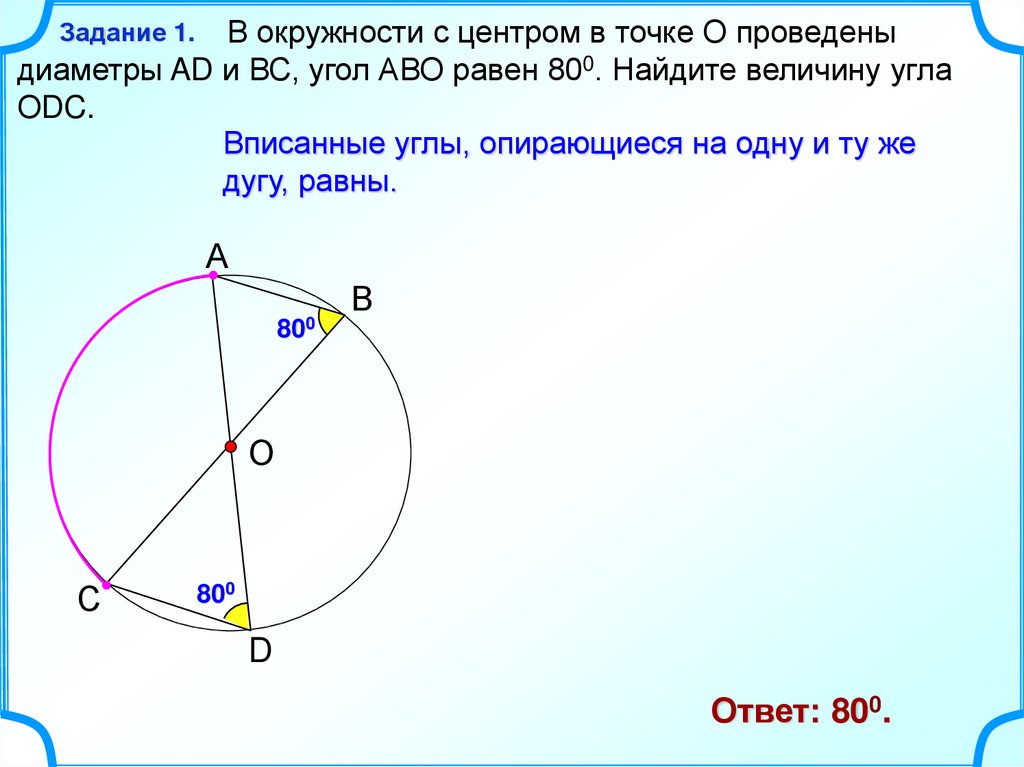
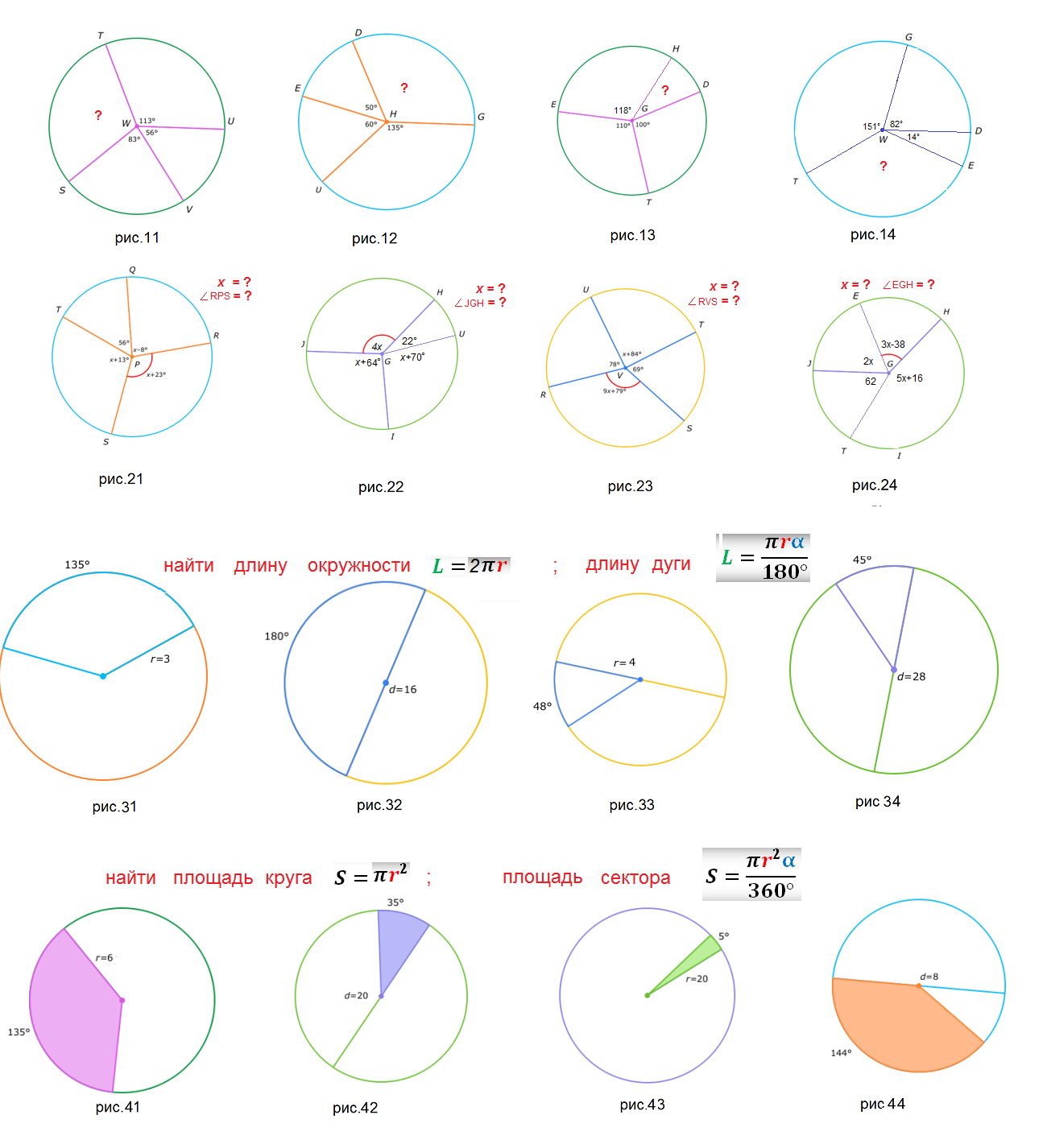
Центральный угол равен дуге, на которую он опирается. Вписанный угол равен половине дуги, на которую он опирается. Ответ дайте в градусах. Рассмотрим картинку:.
- Содержание
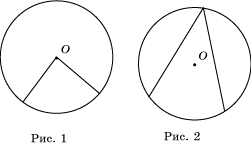
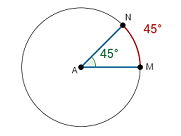
- Центральным углом окружности называется угол, вершина которого находится в центре окружности.
- Справочник по математике Геометрия Планиметрия Углы.
- Математика в школе.
- Центральный угол и дуга: определение
- Угол и окружность: на первый взгляд — ничего общего.
- Вписанный угол — это угол , вершина которого лежит на окружности , а стороны пересекают эту окружность. На теореме о вписанном угле основан метод решения геометрических задач, так называемый метод вспомогательной окружности.
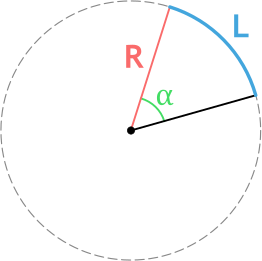
- Дуговым градусом называется часть окружности.
- Математическая связь между центральным углом и дугой
- Удобная навигация, видео-разборы тем, задачи для самопроверки — всё это в вашем кармане.
- Центральный угол — плоский угол с вершиной в центре окружности слева на рисунке.
- Ключевые слова: угол, окружность, хорда, дуга, центральный угол, вписанный угол, касательная, секущая, теорема о секущих, теорема о касательной и секущей, градусная мера дуги, угол опирается на хорду, угол опирается на дугу, дуга стягивает хорду, угол между хордой и касательной, внутренный угол окружности, внешний угол окружности. Центральные и вписанные углы в окружности.
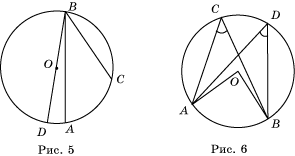




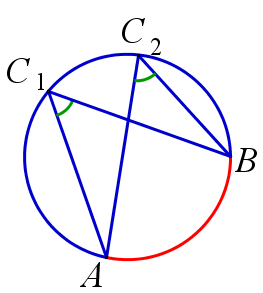
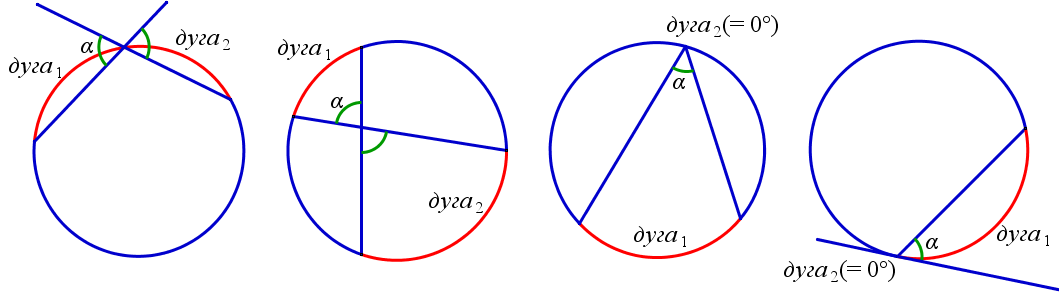
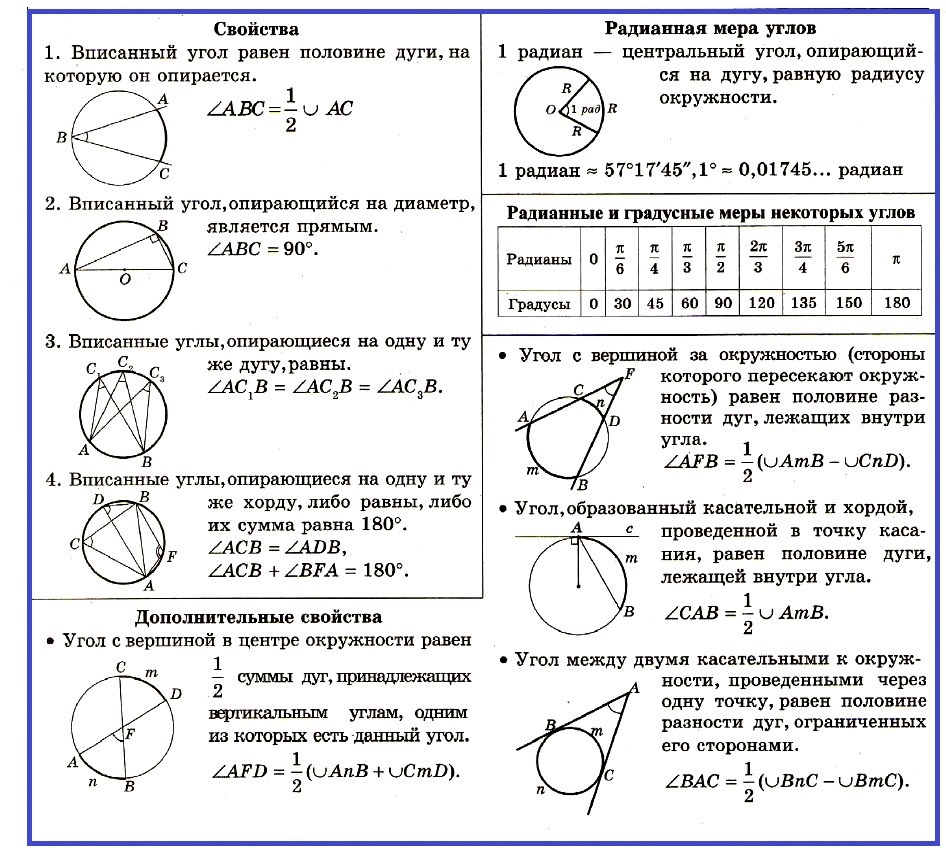

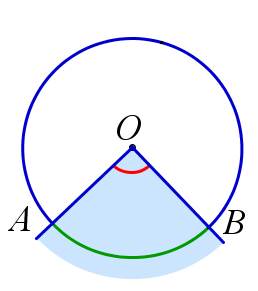
Центральный угол рассматривается вместе со своей внутренней областью — одной из двух частей, на которые стороны угла разбивают плоскость. Градусной мерой дуги окружности называется градусная мера соответствующего ей центрального угла т. Угол называется вписанным в окружность, если его вершина лежит на окружности, а стороны пересекают окружность. Говорят, что вписанный угол опирается на дугу, которую он вместе со своей внутренней областью высекает на окружности. Градусная мера угла, вписанного в окружность, равна половине градусной меры дуги, на которую он опирается, и равна половине градусной меры соответствующего этой дуге центрального угла. Внешний угол вписанного четырёхугольника равен внутреннему углу при противоположной вершине четырёхугольника.