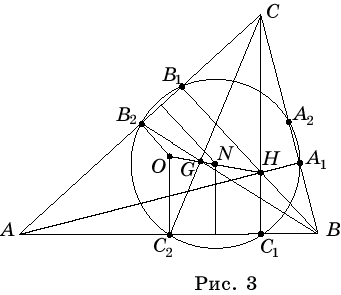
Пересечение высот в треугольнике делится в отношении

Точка пересечения высот треугольника
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними. Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника. Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.


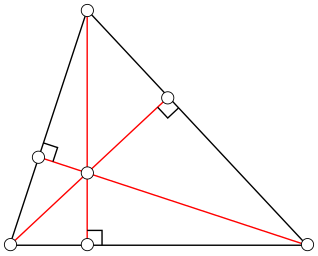
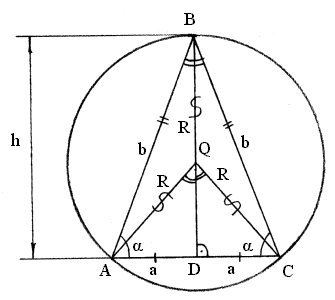


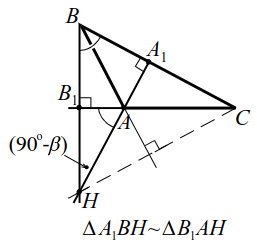


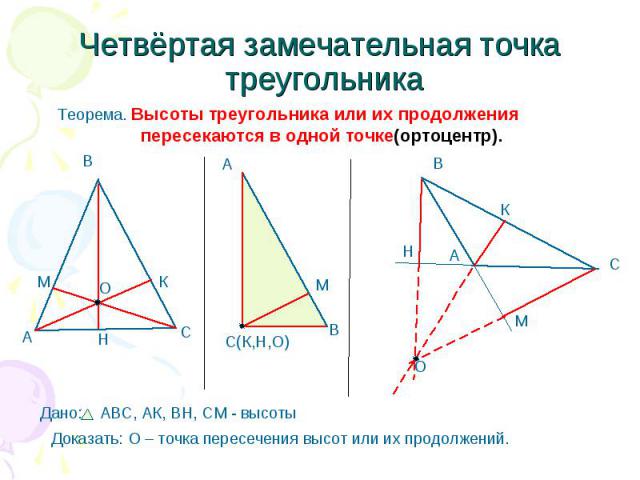
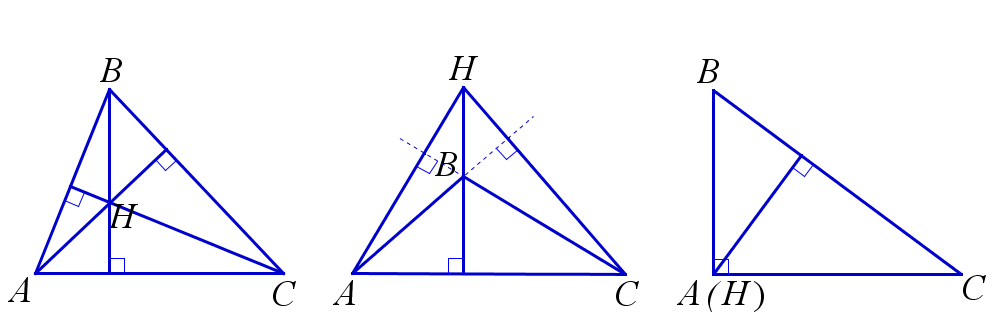
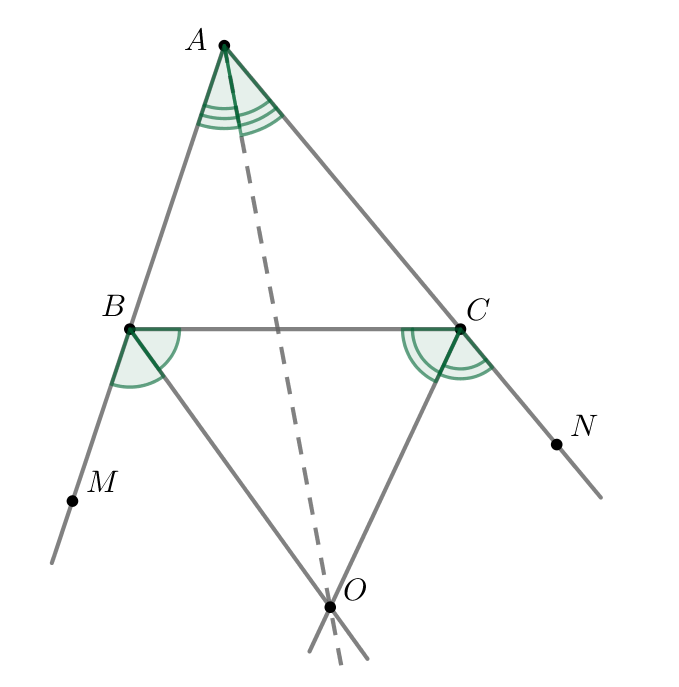
Три биссектрисы треугольника пересекаются в одной точке, которая есть центр вписанной окружности. Три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке, которая есть центр описанной окружности. Три высоты или три прямые , на которых лежат высоты треугольника, пересекаются в одной точке. Эта точка называется ортоцентром треугольника. Если треугольник остроугольный, то каждая из высот есть отрезок, соединяющий вершину и некоторую точку противолежащей стороны.
- Свойства равностороннего треугольника (правильного треугольника)
- Удобная навигация, видео-разборы тем, задачи для самопроверки — всё это в вашем кармане. А ещё раздел с полезными материалами, календарь занятий и уведомления о предстоящих уроках.
- Вход Регистрация.
- Справочник по математике Геометрия Планиметрия Треугольники. Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны рис 1.


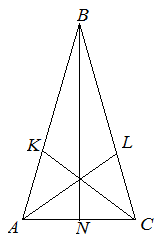




В данной публикации мы рассмотрим основные свойства высоты в равностороннем правильном треугольнике. Также разберем пример решения задачи по этой теме. Примечание: треугольник называется равносторонним , если все его стороны равны. Любая высота в равностороннем треугольнике одновременно является и биссектрисой, и медианой, и серединным перпендикуляром.