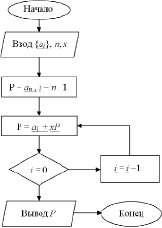
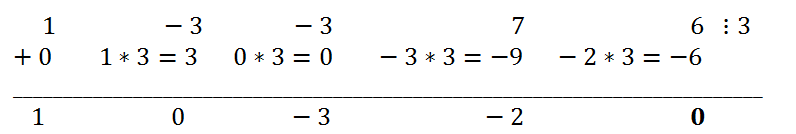Пользуясь схемой горнера разложить полином по степеням

Определить кратность корня x0 многочлена f(x)...
Многочлен первой степени неприводим над любым полем. Многочлен 2-й или 3-й степени приводим над P тогда и только тогда, когда он имеет хотя бы один корень в P. Если приводим над P, то он приводим над любым решением поля P, поэтому при исследовании на приводимость мы начинаем с возможно более узкого поля, над которым определен. Если многочлен неприводим над некоторым полем, то он неприводим над любым его подпольем.
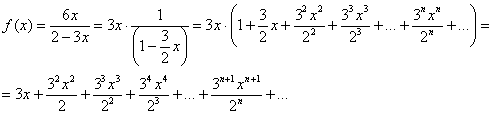









Многочлены от одной переменной и действия над ними. Если а 0, то показатель степени п переменной х называется степенью одночлена. Если одночлен является числом, не равным нулю, то его степень считается равной нулю. Определение 1. Многочленом от одной переменной х называется выражение вида. Если а n 0, то этот многочлен называют многочленом п-й степени от переменной х.
- Разложение полинома по степеням разности х - с.
- Высшая математика — просто и доступно!
- Конев В.
- Деление многочлена на двучлен по схеме Горнера Рассмотрим частный случай деления многочленов — деление многочлена на двучлен вида x - b 0.
- Смотрите также
- Как видно из схемы Горнера количество нулей равно 3, следовательно и кратность равна 3.
- Разложить многочлен f x по степеням x- x 0 и найти значение его производной в точке x 0.
- В данном материале мы рассмотрим как можно разложить произвольный многочлен от одной переменной по степеням. Практические задачи, которые попадаются в учебниках и которые можно решить с помощью бота, выглядят вот так:.
- 6.2.3. Разложение полиномов на множители разных степеней (частичное) над конечными полями
- Работать придётся с таблицей, первая строка которой содержит коэффициенты заданного многочлена они выделены для наглядности синим цветом. Вторая строка таблицы заполняется постепенно.
- Калькулятор ниже делит один многочлен на другой. В результате получаем два многочлена - частное и остаток.
- В этом разделе мы пользуемся теоремой 3. Разложение на сомножители разных степеней Distinct Degree Factorization Вход: — свободный от квадратов полином степени над Выход: Полиномы над такие, что — произведение всех нормированных неприводимых сомножителей степени d полинома 1.



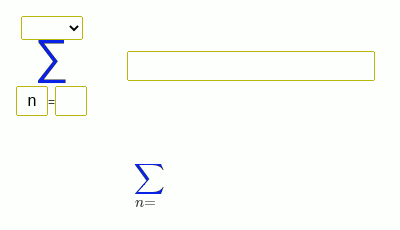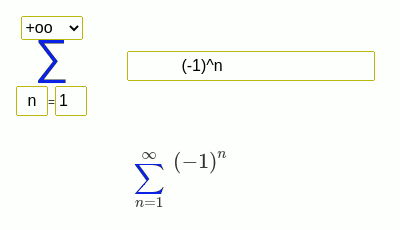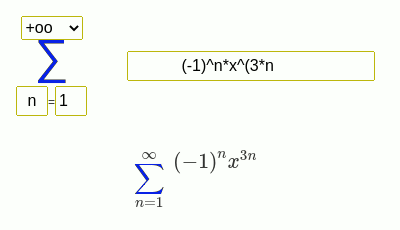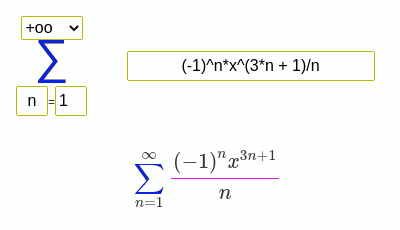
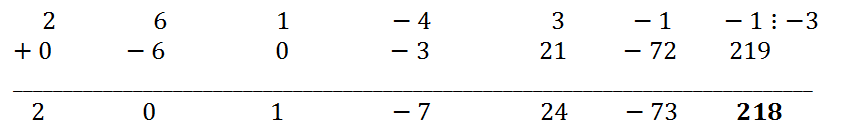


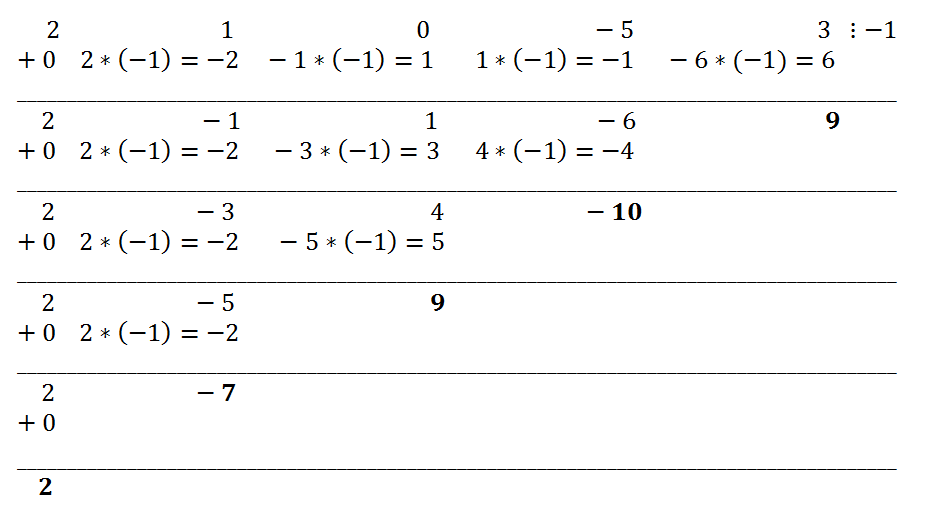
Для начала нужно методом подбора найти один корень. Обычно он является делителем свободного члена. Начнем их подставлять по-очереди:. Мы нашли 1 из корней многочлена.