Задача на эмпирическое корреляционное отношение

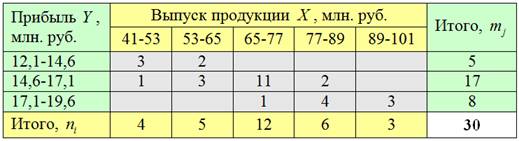
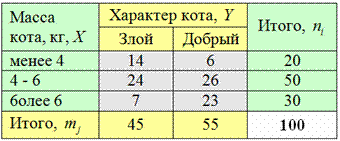
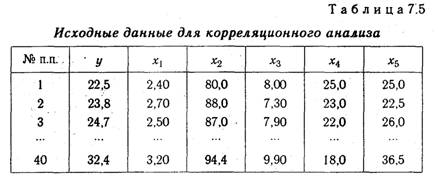
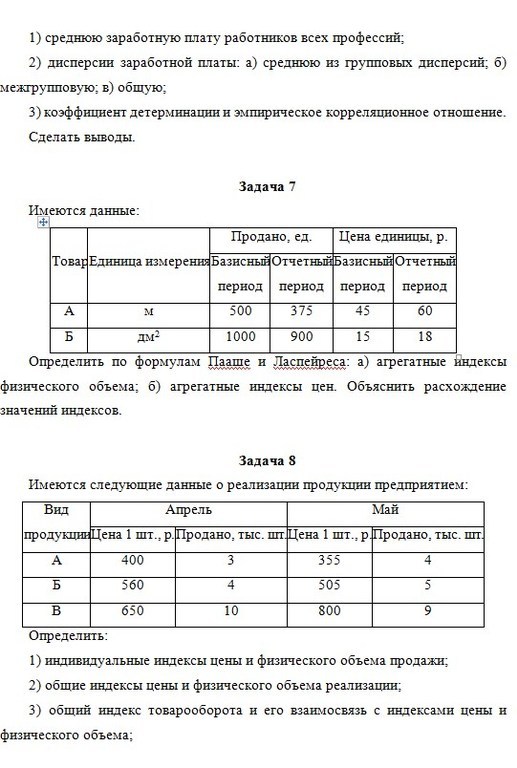
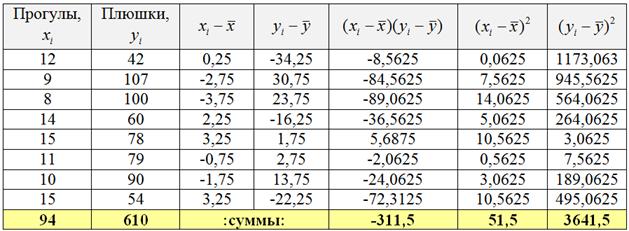
Исходные данные
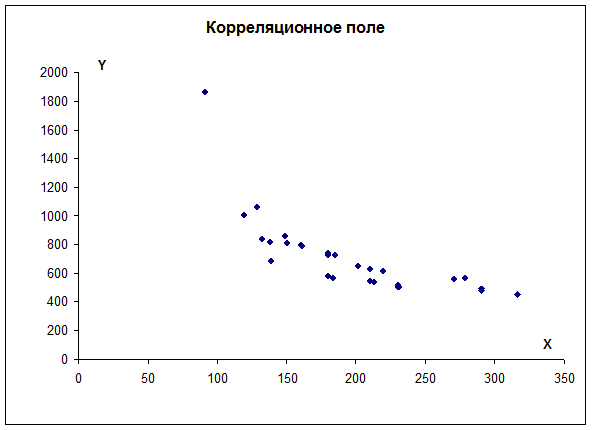
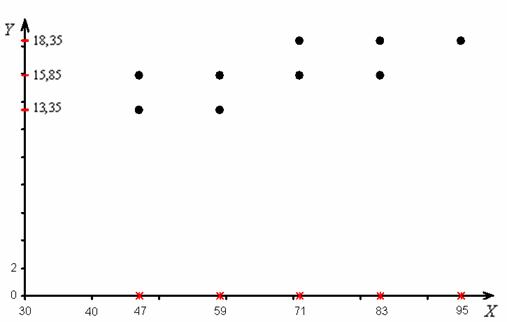
Для оценки тесноты связи между величиной среднедушевого дохода и федеральным округом рассчитаем эмпирическое корреляционное отношение по формуле:. Общая дисперсия признака состоит из межгрупповой дисперсии и средней из внутригрупповых дисперсий:. Расчет групповых средних, внутригрупповой дисперсии и общей дисперсии.


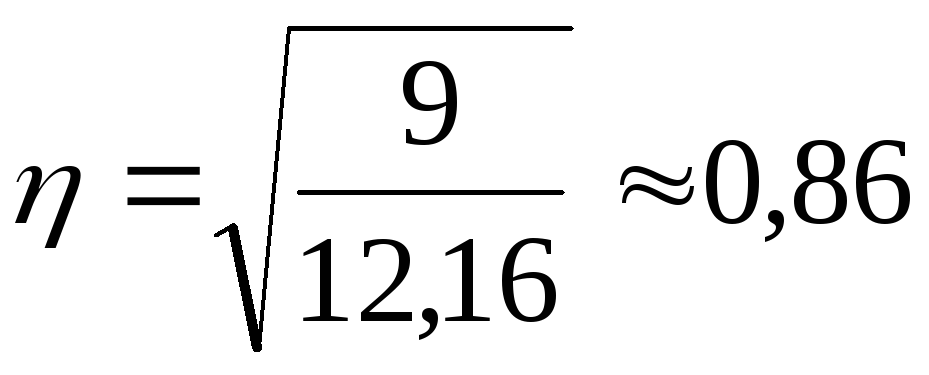



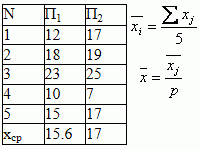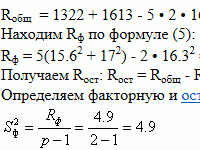
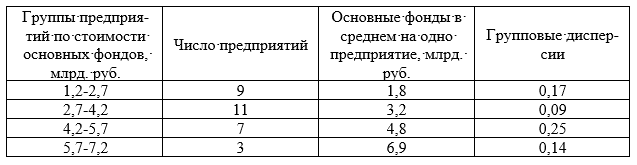

Теперь Кью работает в режиме чтения Мы сохранили весь контент, но добавить что-то новое уже нельзя. Эмпирический коэффициент детерминации равен 0, Чему равно эмпирическое корреляционное отношение? Математика Домашние задания.

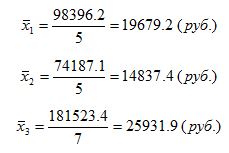
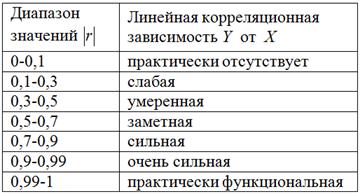


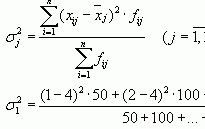


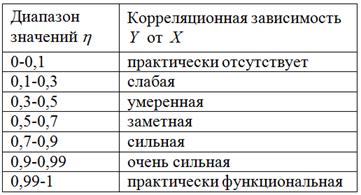
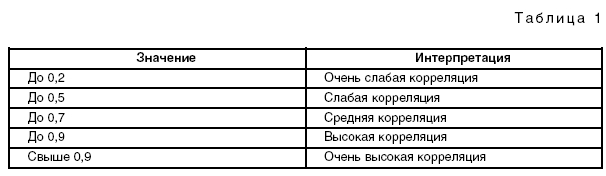
В статистическом анализе широко используется Эмпирический коэффициент детерминации - показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака, и характеризующий силу влияния на образование общей вариации:. Эмпирический коэффициент детерминации показывает долю вариации результативного признака "у" под влиянием факторного признака "х" остальная часть общей вариации "у" обуславливается вариацией прочих факторов. При отсутствии связи эмпирический коэффициент равен нулю, а при функциональной связи - единице. Эмпирическое корреляционное отношение - это корень квадратный из эмпирического коэффициента детерминации:. Эмпирическое корреляционное отношение, как и коэффициент детерминации, может принимать значения от 0 до 1. Если связь отсутствует, то корреляционное отношение равно нулю, то есть все групповые средние будут равны между собой, межгрупповой вариации не будет.